DALL-E (Zero-Shot Text-to-Image Generation) -PART(1/2)
Link to my deep learning blogs : https://rakshithv-deeplearning.blogspot.com/
Last week OpenAI has released DALL-E2 https://twitter.com/OpenAI/status/1511707245536428034?s=20&t=iYtfg3SC-WPupM4IkTeQfA. This system is basically have a capability of generating an image from a text description. Below twitter thread has few examples generated from DALL-E2 https://twitter.com/OpenAI/status/1511714511673126914?s=20&t=4iYWQtFoQ326tSzOyGZcUA. Following is my favourite example :
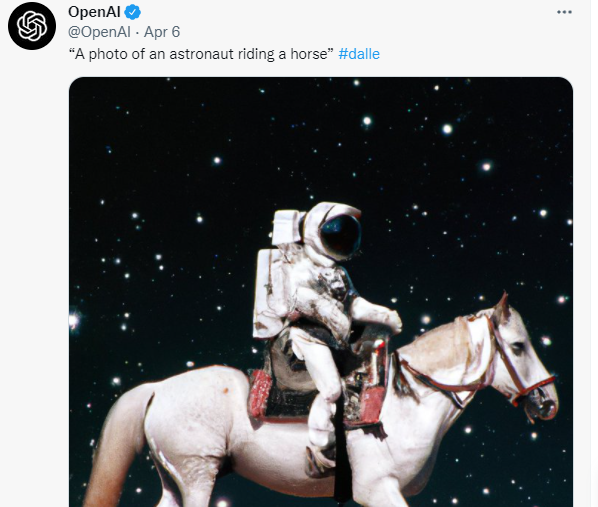
In this blog, I want to discuss technical details of DALL-E (version 1) which was released almost an year ago. I personally felt this paper is content rich than the recent paper. This work is exciting because a system which is trained on image-text pairs is able to generate a very meaningful image from a text which probably hasn’t seen (more like a OOD), of-course this claim could be more appreciable if there is more transparency about the training data which was used, Even though it looks like an amazing progress almost like a magic.
From now-on I only refer to DALL-E (Version 1), this system is composed of two components mainly. First component is d-VAE(discrete-Variational Auto Encoder) and second is Auto-regressive transformer. I will talk about d-VAE in this part-1 and I will write a separate blog about transformer component , results and various engineering details in training the model in part-2.
Main idea is to generate a discrete vector(token) for given image and concatenate with token generated from BPE for text input and feed it into auto-regressive transformer and train a join distribution as shown in the below equation
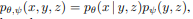
x->image, y->caption and z-> token. This equation gives us an impression that both components are trained together but they aren’t. It was trained separately but for mathematical correctness they have represented the equation in the above format, this was confirmed by first author Aditya Ramesh himself in one of his interview (https://youtu.be/PtdpWC7Sr98).
So, why do they want a discrete token representation for image ?
If we take each pixel of an image as one of the token, then for image of size 256x256x3 memory need to process this is huge-> hence, 256x256 image is represented by 32x32 grid , where each grid represented by a value of one of 8192 tokens (8192 can be treated as a vocab in NLP). So , a single image can be represented by 1024 tokens and concatenated with 256 BPE tokens of a text data.
Now, we get a motivation why it’s important to generate a discrete vector for an image. Now, how do we generate this ? well, there has been some prior work in this direction, VAE(Variational Auto Encoder) is almost a go-to recipe for this kind of application.
(If you are comfortable with VAE and it’s ELBO formulation, you can skip this paragraph).
Before talking about about VAE , I will briefly talk about AE(Auto Encoder) . AE has Encoder-Decoder architecture where encoder takes input X in N-dimensions and represent it in a latent space in D dimension , where D << N. Now, Decoder takes D as input and try to reproduce X^ . Ideally, we want X^ to be as close to X. But this AE can run into over-fitting because of constrained latent mapping. So, there is a much better idea which is VAE. It’s architecture will be similar to AE but difference is that, Now, we try to model the latent space distribution in a different way. Encoder of VAE predicts a mean and variance of a distribution and latent input which is sampled from this distribution will be fed to decoder so it will have better generalization capabilities. If you are interested in understanding this concept with more visualization, you can visit this https://atcold.github.io/pytorch-Deep-Learning/en/week08/08-3/. Sampling operation of VAE is non-differentiable, hence a re-parameterization trick will be used. If you are interested in the mathematical derivation of VAE with ELBO formulation please see this tutorial https://arxiv.org/pdf/1907.08956.pdf (This is one of the cleanest math proofs). Basic approach of this proof is to estimate the posterior distribution of latent space with it’s true distribution. Since true distribution will not be available , by using Baye’s theorem and KL divergence non-zero bound, ELBO can be formulated as a proxy to estimate true distribution.
Now, we have a understanding of how VAE works mathematically we can figure out that latent space output or distribution is not categorical. In DALL-E, input of 256x256x3 image is passed through Resnet and encoder generates a feature map of 32x32x8192, At every grid (32x32) we have a discrete distribution over 8192 tokens. In order to model this - there are some approaches based on VQ-VAE (Vector-Quantized VAE) https://arxiv.org/abs/1711.00937. Idea is that , you have something called codebooks of vocab length V. (Example: if I have a codebook of length 256, each entry in my codebook is basically a vector of some dimension d, so codebook matrix will be 256xd -vector of dimension d is not discrete). Output of encoder will be real valued vectors of dimension d and it will be compared with all 256 vectors in the codebook -then most similar codebook vector will be fed to decoder instead of encoder output, this codebook matrix is learnable.
Similar codebook strategy has been also used in DALL-E but instead of matching the similar codebook vector , Gumbel Soft-max trick is used to sample from categorical distribution (codebook). Folks who have background in self-supervised learning in speech will know about it since it’s been used in wav2vec (https://arxiv.org/abs/2006.11477). What we want here is something like a one-hot vector after passing it through Gumbel Soft-max. We know that Soft-max doesn’t give one-hot distribution, adding temperature parameter to the Soft-max sharpen the distribution but still doesn’t give the one-hot hence essential step is adding Gumbel noise through a re-parametrization trick(separating deterministic and sampling part).
Gumbel distribution = Onehot(argmax(log p + G)), argmax is replaced by Soft-max with temperature . More details are in this paper (https://arxiv.org/pdf/1611.01144.pdf). I do not fully understand the underlying characteristics of Gumbel noise like why adding the Gumbel noise helps in obtaining one-hot . d-VAE component of DALL-E uses this trick to sample from categorical distribution.
Re-construction loss of the d-VAE is setup using Logit Laplace, In general setup image values will be mapped to 0 to 1 and sigmoid is applied at the end of decoder to generate output between 0 to 1. L1 or L2 loss is used in VAE but this may lead to some problem such as distribution produced by neural network is not exactly bounded with input distribution which leads to lot of approximation when further mapping it back to pixel values. In order to over come this instead of a gaussian a Laplacian with bound is defined which will help to map input pixel into defined range and neural network distribution can also be bounded
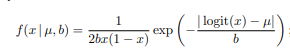
output of a d-VAE decoder outputs both u and b values, x here represents output of decoder. Other training details include Beta term of KL divergence has been increased which found to be quite useful. Network is trained with 64 V100 16GB GPU’s with batch-size of 8 per GPU, AdamW optimizer (Beta1=0.9,Beta=0.99) and learning rate is reduced with cosine decay.
I will continue about auto-regressive transformer in the next part.
Comments
Post a Comment